Главное меню

Экономическая модель оптимального плана производства трех видов изделий, максимизирующего прибыль

x1 + 2x2+ 1x3£ 18.

Аналогично записываются ограничения для других ресурсов:

x1 + 1x2 + 1x3 £ 16

+ 1x2 £ 8

x2 + 1x3 £ 6

Таким образом, математическая модель задачи выглядит следующим образом:

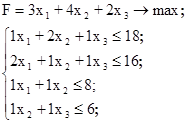
Целевая функция представляет собой общую прибыль от производства продукции. Ограничения отражают конечность запасов ресурсов на предприятии. Неотрицательность переменных следует из их смысла.

Приведем исходную задачу к каноническому виду:

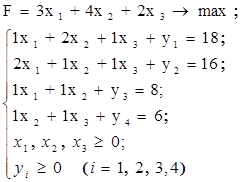
Дополнительные переменные (yi) есть остатки ресурсов каждого вида.

Составим двойственную задачу к математической модели

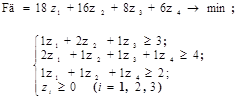
Двойственные переменные - это оценки ресурсов задачи (теневые цены).

Ограничения двойственной задачи приведем к виду равенства:

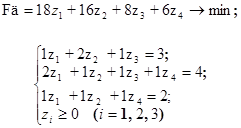
. Решение задачи в Excel с помощью надстройки Поиск решения

Для решения задачи в Excel с помощью надстройки Поиск решения сформируем экран так, как показано на рисунке:

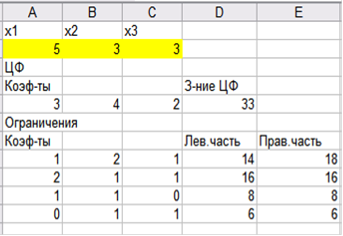
Рисунок 1. Таблица данных для поиска решения

Вызовем надстройку Поиск решения и заполним окно поиска. Необходимо также установить флажок Линейная модель, нажав кнопку Параметры.

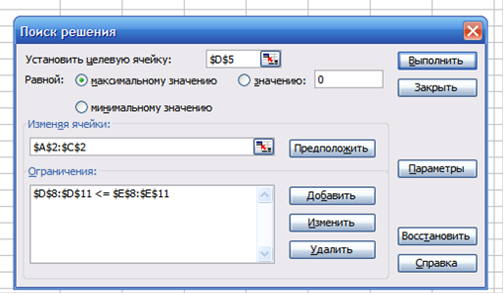
Рисунок 2. Диалоговое окно надстройки «Поиск решения» с реализацией задачи

Затем активизируем процесс поиска и после его окончания в окне Результаты поиска решения выделим все три типа отчетов. Нажатие кнопки OK приведет к созданию новых листов рабочей книги: “Отчет по результатам”, “Отчет по устойчивости” и “Отчет по пределам”. Результаты решения на исходном рабочем листе будут сохранены.

Оптимальные значения всех переменных исходной и двойственной задач с пояснением этих значений в терминах постановки задачи.

Максимальная прибыль в 33 тыс. усл. ед., достигается при сборке изделий:

Изделие I в количестве 5 шт.,